Entanglement chapter 2:
Measurements with entangled photons

In section 1 we have shown that entangled photons are measured consistently as transmitted or reflected at symmetric polarizing beam splitters of Alice’s and Bob’s detectors. So far, their detectors have been set up identically. Next, we will vary the splitting ratio of each beam splitter from 50%:50% to arbitrary values.

Waveplate and beamsplitter

A polarizing beamsplitter (PBS) reflects vertically polarized light (polarization angle 90°) and transmits horizontal polarized light (polarization angle 0°). The transmission properties are identical to the well known Polaroid foils. However, the latter absorbs the rest of the light, whereas with the PBS, the non-transmitted component can be used further. When the polarization angle is different from horizontal, the transmitted power is decreased according to the Malus’ law P(α)= 100%·cos²(α) and the remaining light is reflected (in the case of PBS, or absorbed in the case of Polaroid foils). For a single photon, the power ratio has to be replaced by the transmission probability T(α)= 100%·cos²(α) .
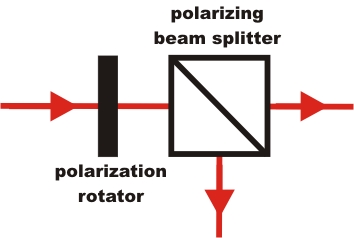
In our experiments, we change the polarization angle with a polarizing rotator (λ/2-plate) (fig. 1). Under rotation of this device, the polarization angle is changed by twice the amount, i.e. a 22.5° physical rotation yields a 45° rotation of the polarization angle. For further details we refer to monographs on classical optics.
Instead of introducing the λ/2-plates, we could simply rotate the polarizing beam splitter and both detectors behind. Obviously, the λ/2-plates are much more convenient from the practical point of view. We will refer to this setup with λ/2-plates as “effectively rotated detectors”. The combination of a λ/2-plate and polarizing beam splitter is a part of Alice's and Bob's side in the experiment (fig. 2).

 

Figure 1: λ/2-plate and polarizing beam splitter: principle (left) and experimental setup (right)

 

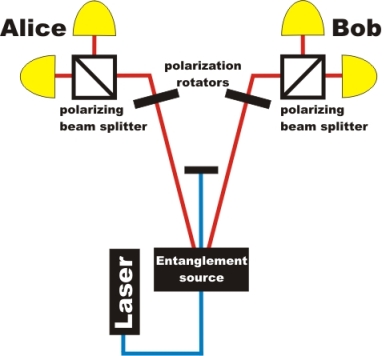
Figure 2: λ/2-plate and polarizing beamsplitter on Alice's and Bob's side

 

 

Entangled photons incident on detectors with effectively rotated detectors

In the following interactive screen experiment (fig. 2), both detectors can be effectively rotated by the same angle in steps of 10°. In the first setting, the incident photon pairs are not entangled; in the second setting the photon pairs are entangled. Observations are completely different for the two cases. The case of different effective rotation for Alice and Bob is shown in the advanced chapter.

 

Observation:
Without entanglement, the horizontal polarized photons are individually transmitted according to Malus’ law as explained above. With entanglement, both photons are transmitted or reflected pair wise. Transmission probability at an individual detector is independent of its effective rotation (i.e. the position of the λ/2-plate).

 

Conclusion

The result of the entanglement experiment cannot be explained in terms of classical optics. The insensitivity with respect to rotation would also be observed with non-polarized light, however random transmission and reflection would happen independently at both detectors. It looks like the photons “would know what the other photon will do”. Entanglement was first discussed as a mathematical prediction of quantum theory and has puzzled many researchers because of the unbelievable consequences. Nobody could believe that photons "talk to each other". Today we can prove in the laboratory that they do not communicate or gain any sort of correlation at their origin in the entanglement crystal. This conundrum is further discussed in section 3.

 

 

Original data: Single Events

To chapter 3: Can entanglement be explained with common sense [klick]?

Back to the overview [klick]

Author: P. Bronner, May 2008